DFG-Projekt zu Schwingungsverhalten von Kreissägeblättern
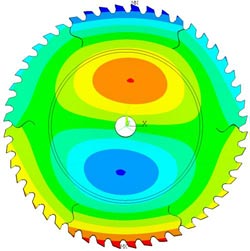
Beispiel für Eigenschwingungsform eines Kreis-sägeblattes . Rot und blau sind die Orte mit maximalen Amplituden. Universität Stuttgart<br>
Von der Metallindustrie über die Steinbearbeitung bis zum Möbelhersteller: Kreissägen kommen in den verschiedensten Wirtschaftsbranchen zum Einsatz. Doch die weit verbreiteten Werkzeuge haben ein Problem: Bei hoher Drehzahl geraten die Sägeblätter in Schwingung und verhalten sich instabil.
Die Folgen sind mangelhafte Oberflächenqualität, ein hoher Nachbearbeitungsaufwand, schnellerer Werkzeugverschleiß und last but not least ein unangenehmes Kreischen. Um dies zu vermeiden, werden Dämpfungsschlitze in die Sägeblätter eingebracht. Diese verschieben die Eigenfrequenzen und verbessern das Verhalten der Sägeblätter beim Abklingen der Schwingungen.
Um die Schlitze optimal auszulegen, sind die Hersteller bisher jedoch auf aufwändige Experimente mit Versuchswerkzeugen und auf Erfahrungswerte angewiesen. Wissenschaftler der Universität Stuttgart untersuchen jetzt, wie die Schwingungen optimal stabilisiert werden können.
Im Rahmen gemeinsamen Forschungsprojekts untersuchen das Institut für Angewandte und Experimentelle Mechanik (IAM) und das Institut für Werkzeugmaschinen (IfW) der Universität Stuttgart den Einfluss der Dämpfungsschlitze und deren Füllmaterialien. Ihr Ziel ist es, für die Zukunft ein wissenschaftlich basiertes Berechnungsmodell bereit zu stellen. Das Vorhaben wird von der Deutschen Forschungsgemeinschaft (DFG) mit rund 500.000 Euro gefördert.
Das Projekt gliedert sich in einen experimentellen und einen numerischen Teil. Ziel der numerischen Forschungsarbeit ist es, Berechnungsmethoden zur Vorhersage von (kritischen) Sägeblatt-Schwingungen bereit zu stellen. Als Verfahren kommt dabei die in der Strukturmechanik bewährte Methode der Finiten Elemente zum Einsatz. Dabei werden sowohl die viskoelastischen Füllmaterialien, als auch die Kreisel-Effekte des rotierenden Sägeblattes berücksichtigt.
Eine numerische Modalanalyse liefert dann die Eigenwerte (Eigenfrequenzen) mit den dazu gehörenden Schwingungsformen sowie das Abklingverhalten der jeweiligen Schwingung. Ist letzteres negativ, handelt es sich um eine instabile Schwingungsform.
Zur Bewertung der Stabilitätsgrenzen kommt ein neues mathematisches Verfahren zum Einsatz, das in Fachkreisen unter der Bezeichnung der Pfadverfolgung bekannt ist. Hierbei werden wesentliche Parameter, wie beispielsweise die Drehzahl als Parameter in das numerische Modell integriert und dann schrittweise erhöht, was die Grundlage für eine optimierte Konfiguration von Kreissägeblättern schafft. In einem Teilbereich des Forschungsvorhabens untersuchen die Wissenschaftler darüber hinaus das Geschehen an der Schnittstelle von Sägeblatt, Flansch und Kreissägemaschine, um Voraussagen auf das statische und dynamische Verhalten machen zu können.
In jedem Arbeitsschritt werden die Simulationen experimentellen Untersuchungen gegenübergestellt, um zu jedem Zeitpunkt die Modellparameter anpassen zu können. Zum Ende des Projekts wird ein validiertes Modellierungsverfahren existieren, das eine Voraussage des statischen und dynamischen Verhaltens von Sägeblättern erlaubt. Darüber hinaus soll dem Konstrukteur von Kreissägeblättern ein Simulationstool an die Hand gegeben werden, das wissenschaftlich abgesicherte Methoden und Richtlinien zum optimalen Werkzeugdesign hinsichtlich der Schlitzkonfiguration, Füllstoffe und Einspannbedingungen anwendet. Globales Ziel des Forschungsvorhabens ist es, das Verhalten des Kreissägeblattes grundlegend zu verstehen, um zukünftig ein an die jeweils vorliegenden Anwendungen angepasstes und optimiertes Kreissägeblatt entwickeln zu können.
Weitere Informationen:
Dr. André Schmidt, Universität Stuttgart, Institut für Angewandte und Experimentelle Mechanik (IAM), Tel. 0711/685-66275, E-Mail andre.schmidt (at) iam.uni-stuttgart.de
Dr. Thomas Stehle und Simon Weiland, Universität Stuttgart, Institut für Werkzeugmaschinen (IfW), Tel. 0711/685-83866/ 84560, E-Mail thomas.stehle (at) ifw.uni-stuttgart.de, simon.weiland (at) ifw.uni-stuttgart.de
Als viskoelastisch bezeichnet man Stoffe mit teilweise elastischem und teilweise viskosem Materialverhalten.
Media Contact
Weitere Informationen:
http://www.uni-stuttgart.deAlle Nachrichten aus der Kategorie: Materialwissenschaften
Die Materialwissenschaft bezeichnet eine Wissenschaft, die sich mit der Erforschung – d. h. der Entwicklung, der Herstellung und Verarbeitung – von Materialien und Werkstoffen beschäftigt. Biologische oder medizinische Facetten gewinnen in der modernen Ausrichtung zunehmend an Gewicht.
Der innovations report bietet Ihnen hierzu interessante Artikel über die Materialentwicklung und deren Anwendungen, sowie über die Struktur und Eigenschaften neuer Werkstoffe.
Neueste Beiträge

Anlagenkonzepte für die Fertigung von Bipolarplatten, MEAs und Drucktanks
Grüner Wasserstoff zählt zu den Energieträgern der Zukunft. Um ihn in großen Mengen zu erzeugen, zu speichern und wieder in elektrische Energie zu wandeln, bedarf es effizienter und skalierbarer Fertigungsprozesse…

Ausfallsichere Dehnungssensoren ohne Stromverbrauch
Um die Sicherheit von Brücken, Kränen, Pipelines, Windrädern und vielem mehr zu überwachen, werden Dehnungssensoren benötigt. Eine grundlegend neue Technologie dafür haben Wissenschaftlerinnen und Wissenschaftler aus Bochum und Paderborn entwickelt….

Dauerlastfähige Wechselrichter
… ermöglichen deutliche Leistungssteigerung elektrischer Antriebe. Überhitzende Komponenten limitieren die Leistungsfähigkeit von Antriebssträngen bei Elektrofahrzeugen erheblich. Wechselrichtern fällt dabei eine große thermische Last zu, weshalb sie unter hohem Energieaufwand aktiv…





















